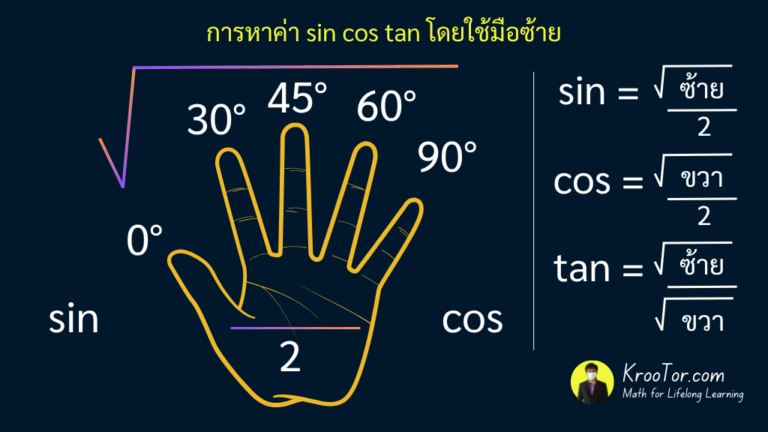
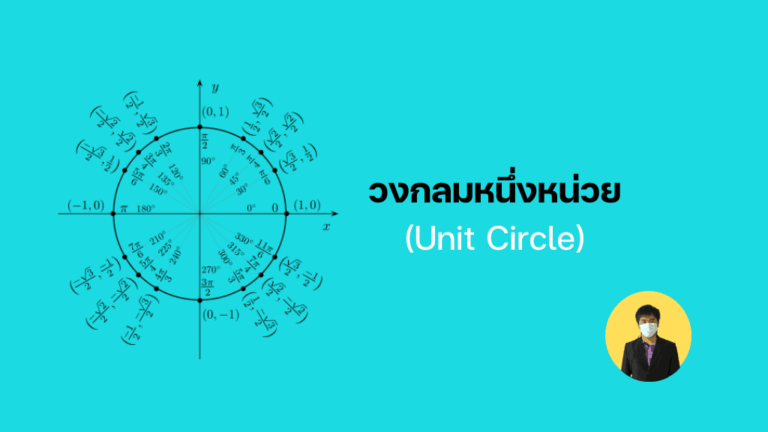
1. สูตรตรีโกณมิติพื้นฐาน
sin θ = ด้านตรงข้ามมุม θ / ด้านตรงข้ามมุมฉาก
cos θ = ด้านประชิดมุม θ / ด้านตรงข้ามมุมฉาก
tan θ = ด้านตรงข้ามมุม θ / ด้านประชิดมุม θ
cosec θ = ด้านตรงข้ามมุมฉาก / ด้านตรงข้ามมุม θ
sec θ = ด้านตรงข้ามมุมฉาก / ด้านประชิดมุม θ
cot θ = ด้านประชิดมุม θ / ด้านตรงข้ามมุม θ
2. เอกลักษณ์ปีทาโกรัส (Pythagorean Identities)
ตามทฤษฎีบทพีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ถ้า c คือด้านตรงข้ามมุมฉาก และ a, b เป็นด้านประกอบมุมฉาก ดังนั้น c2 = a2 + b2 เราสามารถใช้เอกลักษณ์พีทาโกรัสได้ โดยใช้ทฤษฎีบทและอัตราส่วนตรีโกณมิติ สูตรนี้จะใช้ในการแปลงอัตราส่วนตรีโกณมิติหนึ่งไปเป็นอัตราส่วนอื่น
sin2 θ + cos2 θ = 1
1 + tan2 θ = sec2 θ
1 + cot2 θ = cosec2 θ
3. สูตรผลบวกและผลต่าง
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
