ดอกเบี้ยทบต้น (Compound interest) เป็นดอกเบี้ยที่ใช้ในสถาบันการเงิน เช่น การกู้เงิน หรือการฝากเงินกับทางธนาคาร เป็นดอกเบี้ยที่ใช้กันทั่วไปในชีวิตประจำวัน
ดอกเบี้ยทบต้นคืออะไร?
ดอกเบี้ยทบต้น คือดอกเบี้ยที่คิดจากการเอาดอกเบี้ยในรอบที่ผ่านมา รวมกับเงินต้นเดิม แล้วคิดเป็นเงินต้นใหม่ในรอบปัจจุบัน ทบเป็นเงินต้นกันไปเรื่อยๆ
สูตรคำนวณดอกเบี้ยทบต้น
สูตรดอกเบี้ยทบต้น (Compound Interest Formula) สามารถคำนวณหาเงินรวมทั้งหมดที่จะได้รับจากสูตร
\text{A}=\text{P}\left (1+\frac{r}{n} \right )^{nt}
เมื่อ A แทนเงินรวม, P แทนเงินต้น, r แทนอัตราดอกเบี้ยต่อปี (หน่วยทศนิยม), n แทนจำนวนครั้งที่จ่ายดอกเบี้ยต่อปี และ t แทนระยะเวลา (ปี)
อัตราดอกเบี้ย (r) ต้องเปลี่ยนจากเปอร์เซ็นต์ (%) ให้อยู่ในรูปทศนิยม โดยการหารด้วย 100 เช่น ดอกเบี้ย 5% จะเท่ากับ 5÷100 = 0.05 (อ่านเพิ่มเติม: การเขียนเปอร์เซ็นต์ให้อยู่ในรูปทศนิยม)
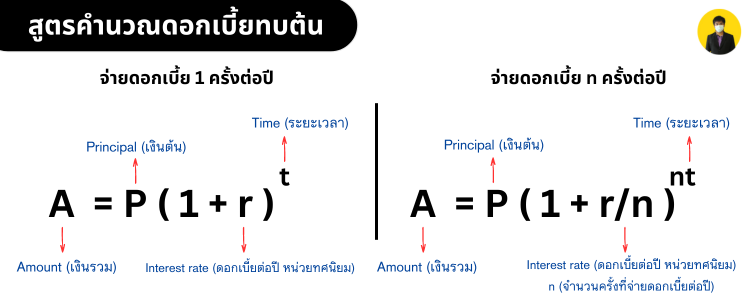
สูตรคำนวณอัตราดอกเบี้ยทบ สามารถคำนวณได้ในสถานการณ์ต่างๆ เช่น อัตราดอกเบี้ยทบต้นรายปี รายครึ่งปี รายไตรมาส รายเดือน รายวัน ฯลฯ
สำหรับบัญชีเงินฝากกับธนาคารในประเทศไทย ส่วนใหญ่จะจ่ายดอกเบี้ยอยู่ที่ 2 ครั้งต่อปี คือในช่วงเดือน มิ.ย. และ ธ.ค. ของทุกปี สามารถดูได้ตามสูตรด้านล่างนี้
ตัวอย่างสูตรดอกเบี้ยทบทบตามจำนวนครั้งที่จ่ายต่อปี
| จำนวนครั้งที่คิดดอกเบี้ยต่อปี | สูตรคำนวณ |
|---|---|
| 1 ครั้ง/ปี | \text{A}=\text{P}\left (1+r \right )^{t} |
| 2 ครั้ง/ปี | \text{A}=\text{P}\left (1+\frac{r}{2} \right )^{2t} |
| 3 ครั้ง/ปี | \text{A}=\text{P}\left (1+\frac{r}{3} \right )^{3t} |
| 4 ครั้ง/ปี | \text{A}=\text{P}\left (1+\frac{r}{4} \right )^{4t} |
| 6 ครั้ง/ปี | \text{A}=\text{P}\left (1+\frac{r}{6} \right )^{6t} |
| 12 ครั้ง/ปี (รายเดือน) | \text{A}=\text{P}\left (1+\frac{r}{12} \right )^{12t} |
| 365 ครั้ง/ปี (รายวัน) | \text{A}=\text{P}\left (1+\frac{r}{365} \right )^{365t} |
ตัวอย่างการคำนวณดอกเบี้ยทบต้น
ตัวอย่างการใช้สูตรคำนวณดอกเบี้ยเงินฝาก
ตัวอย่าง 1 ฝากเงิน 10,000 บาท อัตราดอกเบี้ยทบต้น 0.5% ต่อปี ธนาคารจ่ายดอกเบี้ย 1 ครั้งต่อปี เมื่อเวลาผ่านไป 5 ปี จะมีเงินรวมทั้งหมดกี่บาท
วิธีทำ จากโจทย์ เงินต้น (P) = 10,000 บาท, อัตราดอกเบี้ย (r) 0.5% = 0.005 และเวลา (t) = 5 ปี
\begin{align*} \text{A} & = \text{P} \left (1+r \right )^{t} \\ \text{A} & = 10,000 \left (1+0.005 \right )^{5} \\ & = 10,000 \left (1.005 \right )^{5} \\ & \approx 10,252.51 \\ \end{align*}ดังนั้น เมื่อฝากเงินครบ 5 ปี จะมีเงินรวม 10,252.51 บาท
ตัวอย่าง 2 ครูโต๋ฝากเงิน 150,000 บาท ในบัญชีธนาคารกสิกรไทย ประเภท eSavings อัตราดอกเบี้ย 1.5% ต่อปี โดยจ่ายดอกเบี้ยทุก 6 เดือน เมื่อฝากครบ 3 ปี จะได้รับเงินต้นพร้อมดอกเบี้ยเป็นจำนวนเงินกี่บาท
วิธีทำ จากโจทย์ เงินต้น (P) = 150,000 บาท, อัตราดอกเบี้ย (r) 1.5% = 0.015, จ่ายดอกเบี้ย 2 ครั้งต่อปี (n) =2 และเวลา (t) = 3 ปี
\begin{align*} \text{A} &=\text{P}\left (1+\frac{r}{n} \right )^{nt} \\ &=150,000 \left (1+\frac{0.015}{2} \right )^{2(3)} \\ &=150,000 \left (1.0075 \right )^{6} \\ & \approx 156,877.84 \\ \end{align*}ดังนั้น เมื่อฝากเงินครบ 3 ปี ครูโต๋จะมีเงินรวม 156,877.84 บาท
ตัวอย่าง 3 ภัทร์ฝากเงินที่สหกรณ์ออมทรัพย์จำนวน 30,000 บาท โดยสหกรณ์ให้ดอกเบี้ย 3% ต่อปี และจ่ายดอกเบี้ยทบต้นทุก 4 เดือน ถ้าภัทร์ฝากเงินจำนวนนี้เป็นเวลา 8 เดือน แล้วภัทร์จะมีเงินฝากเพิ่มขึ้นกี่บาท [O-net ม.6 มี.ค.64]
วิธีทำ จากโจทย์ เงินต้น (P) = 30,000 บาท, อัตราดอกเบี้ย (r) 3% = 0.03, จ่ายดอกเบี้ย 3 ครั้งต่อปี (n) = 3 และเวลา (t) = 8/12 = 2/3 ปี
\begin{align*} \text{A} &=\text{P}\left (1+\frac{r}{n} \right )^{nt} \\ &=30,000 \left (1+\frac{0.03}{3} \right )^{3(\frac{2}{3})} \\ &=30,000 \left (1+0.01 \right )^{2} \\ &=30,000 \left (1.01 \right )^{2} \\ &=30,000 \left (1.0201 \right ) \\ & =30,603 \\ \end{align*}เมื่อฝากเงินครบ 8 เดือน ภัทร์จะได้รับเงินรวม 30,603 บาท
ดังนั้น ภัทร์จะมีเงินฝากเพิ่มขึ้น 603 บาท