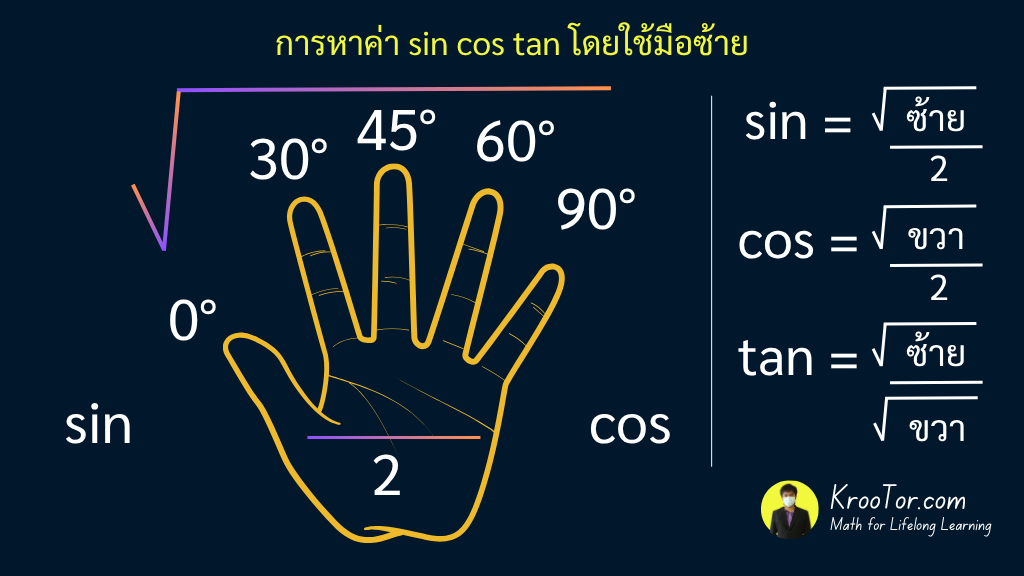
การเรียนรู้ฟังก์ชันตรีโกณมิติอย่าง Sine (sin), Cosine (cos) และ Tangent (tan) อาจดูซับซ้อนในช่วงแรก แต่มีเทคนิคง่ายๆ ที่ช่วยให้จดจำค่าเหล่านี้ได้อย่างรวดเร็ว นั่นคือ เทคนิค “มือซ้าย” ที่ใช้แค่ฝ่ามือ ก็สามารถจำค่า sin cos tan ของมุมพื้นฐาน 0°, 30°, 45°, 60°, และ 90° ได้แล้ว
การใช้มือซ้ายหาค่า sin, cos, tan
1. กางมือซ้ายขึ้นมา
- กางมือซ้ายหันฝ่ามือเข้าหาตัวเอง
- นิ้วแต่ละนิ้วแทนมุมต่างๆ ดังนี้:
| นิ้ว | มุมที่แทน |
|---|---|
| นิ้วโป้ง | 0° |
| นิ้วชี้ | 30° |
| นิ้วกลาง | 45° |
| นิ้วนาง | 60° |
| นิ้วก้อย | 90° |
2. การหาค่า sin(θ)
- พับนิ้วที่แทนมุมที่ต้องการลง
- นับจำนวนนิ้วที่อยู่ ด้านซ้ายของนิ้วที่พับ แล้วนำจำนวนนี้ไปแทนในสูตร:
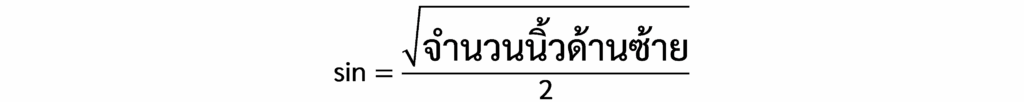
ตัวอย่าง:
- ต้องการหา sin(30°) → พับนิ้วชี้ลง เหลือนิ้วด้านซ้าย 1 นิ้ว
$$\sin(30°) = \frac{\sqrt{1}}{2} = \frac{1}{2}$$
3. การหาค่า cos(θ)
- ใช้วิธีเดียวกัน แต่ให้นับนิ้วที่อยู่ ด้านขวาของนิ้วที่พับ
- สูตรคือ:
ตัวอย่าง:
- cos(30°) → พับนิ้วชี้ลง เหลือนิ้วด้านขวา 3 นิ้ว
\cos(30°) = \frac{\sqrt{3}}{2}4. การหาค่า tan(θ)
เมื่อรู้ค่า sin และ cos แล้ว สามารถหา tan ได้ง่ายๆ ด้วยสูตร: \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} หรือใช้สูตร
ตัวอย่าง:
tan(45°) → พับนิ้วกลางลง เหลือนิ้วด้านขวา 2 นิ้ว และนิ้วด้านซ้าย 2 นิ้ว
$$\tan(45°) = \frac{\sqrt{2}}{\sqrt{2}} = 1$$
สรุปค่าตรีโกณมิติ
| มุม (°) | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 หรือ √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | ไม่นิยาม |
